Motion Along a Straight Line
Objectives
In this chapter we will study one dimensional kinematics i.e. how objects move along a straight line:
The following parameters will be defined:
Displacement
Average velocity
Average Speed
Instantaneous velocity
Average and instantaneous acceleration
We will learn how direction of acceleration with respect to direction of velocity, affects the magnitude of velocity.
How to compute velocity from displacement vs. Time graph.
How to compute acceleration from velocity vs. Time graph.
We will develop the kinematic equations that give us the velocity and position at any time for constant acceleration.
We will learn to compute displacement from velocity vs. Time graph for any value of acceleration.
We will learn to compute change in velocity from acceleration vs. Time graph for any value of acceleration.
What is a one dimensional motion?
Observe (click play) the motion of three disks.
What is common in motions of these discs?
Can we say that all the three were moving in one dimension?
Answer is NO. Why?
When an object moves in a straight line along a single axis. Such a motion is called one-dimensional motion.
Can we tell, which of the three discs were performing one dimensional motion?
Blue is moving in a straight line along Vertical axis (y-axis).
Green is moving in straight line along horizontal axis (x-axis).
Therefore we can say that only blue and green are performing one-dimensional motion.
Forces cause motion but we will not discuss cause of motion in this chapter, we will only discuss the motion itself and change in motion.
These discs could represent any rigid object or a particle.
What is a rigid object?
An object whose shape stays same as it moves is called a rigid body or object.
An ideal rigid body is nonexistent.
An object in which the atomic forces are so strong that the little force needed to move it do not bend it, can be considered a rigid body.
Position
How we locate an object?
We try to find its position relative to some reference point (origin or zero point) of an axis.

The positive direction of the axis is in the direction of increasing numbers, which is in the right
The opposite is the negative direction.
Position is a vector quantity as it has direction (+ or – in one dimension) and magnitude.
What is the position of Green, Orange and Blue disks?
Green is -4 m, Red is -2 m and Blue is +4 m.
Displacement
What is the position of red disc?
Move (click play) it to a new position.
Displacement is the change from one position ![]() to another position
to another position ![]() .
.
Displacement is a vector quantity with direction (+ or – in one dimension) and magnitude.
How displacement is computed?
Displacement is computed by subtracting initial position ![]() from final position
from final position ![]() .
.
![]()
Symbol Δ (uppercase delta), represents a change in quantity (here it is change in position)
What will be displacement if object moves from ![]() to
to ![]() ?
?
![]()
What is the direction of motion?
Positive sign of Δx indicates that the motion is along the positive x-direction
What will be displacement if the object moves from ![]() to
to ![]() ?
?
![]()
What is the direction of motion?
Negative sign of Δx indicates that the motion is along the negative x-direction
Displacement vs. Total Distance
Watch the motion of red disk below (click play).
Blue arrow is the instantaneous displacement.
The disk moved from initial position ![]() to
to ![]() . Even though the total distance (dotted line) covered is 10 m the displacement is still Δx = 0.
. Even though the total distance (dotted line) covered is 10 m the displacement is still Δx = 0.
![]()
Now watch the motion of blue disk (click play) below.
Red arrow is the displacement.
The disk moved from initial position ![]() to
to ![]() . Even though the total distance (dotted line) covered is 8 m the displacement is Δx = 2m.
. Even though the total distance (dotted line) covered is 8 m the displacement is Δx = 2m.
![]()
The actual distance for a trip is irrelevant as far as the displacement is concerned
Position time Graph
Position of a moving object (blue disk) can be plotted as a function of time.
Note down position of moving disk (blue) for different values of time t.
These various noted values of points (t, x) can be plotted as a graph with position x(t) at a given time t on Vertical axes and time t on horizontal axes.
This is called time versus position graph or position time graph.
Stationary Object
When the position of an object or a particle does not change with time, it is called a stationary object or particle.
What we observed?
In other words displacement of the particle is zero with time.
![]()
Position time graph of a stationary object is parallel to time axes.
The position of the object stays at x=-5 m for 10 s.
Average Velocity
Average velocity ![]() , is the ratio of the displacement Δx that occurs during a particular time interval Δt to that interval.
, is the ratio of the displacement Δx that occurs during a particular time interval Δt to that interval.
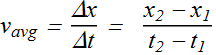
On a position x versus t graph, ![]() is the slope of the straight line (Magenta line) that connects two particular points on the x (t) curve : one point is (
is the slope of the straight line (Magenta line) that connects two particular points on the x (t) curve : one point is (![]() ,
, ![]() ), and other point is
), and other point is ![]()
Average Speed
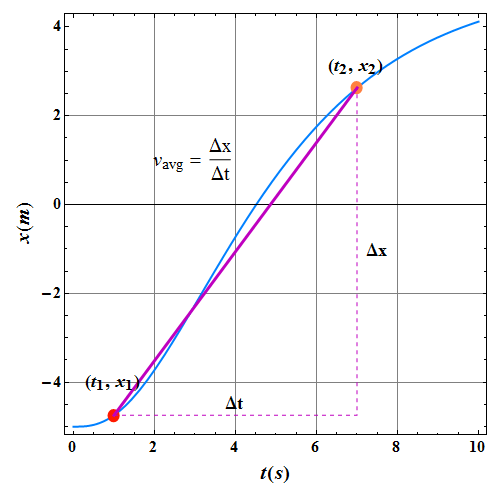
Average speed ![]() , is the ratio of the total distance covered during a particular time interval Δt to that interval.
, is the ratio of the total distance covered during a particular time interval Δt to that interval.
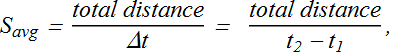
Average speed does not include direction, it lacks any algebraic sign.
Some time ![]() is the same (except for the absence of sign) as
is the same (except for the absence of sign) as ![]() . As in the following example.
. As in the following example.
In the above example Δx = 5 m and total distance covered is also 5 m.
However (following example) when an object double back on its path, the two can be quite different.
In the above example Δx = 2 m (red arrow) while total distance covered is 8 m.
Instantaneous Velocity and Speed
Instantaneous velocity v is the change in particle position x with time at a given instant.
How to compute instantaneous velocity?
First calculate average velocity around the given instant (red circle).
Now shrink the time interval Δt (using Δt slider) closer and closer to 0.
As Δt becomes shorter and shorter the average velocity approaches a limiting value, which is the instantaneous velocity (or simply velocity).
Mathematically v is the derivative of x with respect to t.
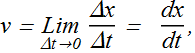
In graphical term, velocity v at given instant is the slope of the particle’ s position - time curve at the point representing that instant.
Instantaneous speed (Speed) is the magnitude of velocity.
Time vs. Velocity Graph
We are given a position time graph, how can we obtain velocity time graph from this?
We can measure slope of the curve at each time position (red circle).
Value of slope is velocity v at that instant (time).
These various noted values of points (t, v) can be plotted as a graph with velocity v(t) on Vertical axes and time t on horizontal axes.
Acceleration
When a particle's velocity changes, the particle is said to undergo acceleration (or to accelerate).
For motion along an axis, the average acceleration ![]() over a time interval Δt is defined as
over a time interval Δt is defined as
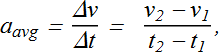
![]() is the particle velocity at time
is the particle velocity at time ![]() and
and ![]() is particle velocity at
is particle velocity at ![]() .
.
The instantaneous acceleration (or simply acceleration) is the derivative of the velocity with respect to time:
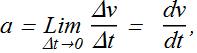
Acceleration of a particle at any instant is the rate at which its velocity is changing at that instant.
Units of Acceleration
We found that acceleration is derivative of velocity with time.
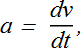
Now velocity is derivative of position x(t) with time, therefore at any instant acceleration is the second derivative of its position x(t) with respect to time.
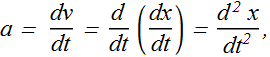
Unit of acceleration is the m/(s.s) or ![]() .
.
Information from sign of Acceleration
Positive sign of acceleration indicates it is acting to the right and negative sign indicates it is acting to the left.
Just form the sign of acceleration, can we tell whether an object's speed is increasing or decreasing?
Answer is "No"., Why?
We need to know sign of velocity too.
If the signs of the velocity and acceleration of a particle are the same, the speed of the particle increases. If the signs are opposite, the speed decreases.
Time vs. Acceleration Graph
We have a velocity time graph, how can we obtain acceleration time graph from this?
We can measure slope of the curve at each time position (red circle).
Value of slope is acceleration a at that instant (time).
These various noted values of points (t, a) can be plotted as a graph with acceleration a(t) on Vertical axes and time t on horizontal axes.
Constant Acceleration
Let us explore how various graphs look like for different values of velocity and acceleration.
When acceleration is constant, how the slope of velocity time graph change with time?
It is constant.
Equations of Motion (Kinematic Equations)
When the acceleration is constant, the average acceleration is equal to the instantaneous acceleration.
![]()
![]()
Here ![]() is the velocity at time t=0 and v is the velocity at any later time t.
is the velocity at time t=0 and v is the velocity at any later time t.
For constant acceleration the average velocity ![]() over a time interval t can also be given as the average of the initial velocity
over a time interval t can also be given as the average of the initial velocity ![]() and final velocity v.
and final velocity v.
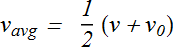
When ![]() is the initial position and x is the position at time t, then average velocity
is the initial position and x is the position at time t, then average velocity ![]() is given as
is given as
![]()
Combining above equations we get
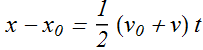
Kinematic Equations
For Constant acceleration, with the help of above two equations we can find following list of equations of motion.
| Equation | Quantity Missing |
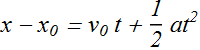 |
v |
| t | |
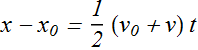 |
a |
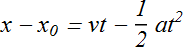 |
All these equations are only valid for constant acceleration.
Free Fall Acceleration
Free fall acceleration is an example of constant acceleration.
When we toss an object either up or down and could somehow eliminate the effects of air on its flight, we would find that the object accelerates downward at a constant rate.
That rate is called the free-fall acceleration, and its magnitude is represented by g.
The free-fall acceleration is negative: that is, downward on the y axis, toward Earth's center.
The free-fall acceleration near Earth's surface is ![]() , and the magnitude of the acceleration is
, and the magnitude of the acceleration is ![]() . Do not substitute
. Do not substitute ![]() for g.
for g.
Graphical Integration in Motion Analysis
Can we calculate the displacement, if we know time versus velocity graph representing motion of a particle?
Yes, we can compute the displacement between any time interval (![]() to
to ![]() )
)
Velocity v is defined as derivative of position with time.
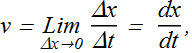
In other words for a very small interval of time (Δt→0), the displacement Δx can be given as
![]()
Example 1:
Suppose the time versus velocity plot of a moving object is as follow.
If we want to compute displacement from initial time ![]() to final time
to final time ![]() , we can divide this time into four equal parts of Δt=0.5s each (Select Show).
, we can divide this time into four equal parts of Δt=0.5s each (Select Show).
Now total displacement will be the sum of displacement in these four small intervals.
![]()
To increase the accuracy of our calculations, we need to make Δt as small as possible, therefore the displacement will be
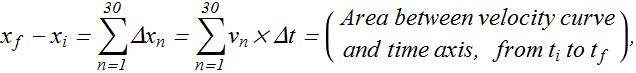
For further accuracy we can make Δt very small (Δt→0) and Fundamental Theorem of Calculus tells us that
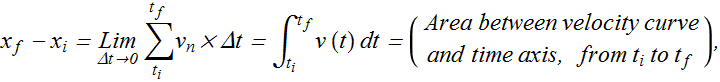
Example 2 :
When we have a graph of an object's time versus acceleration, we can integrate on the graph to find the object's velocity at any given time (If initial or final velocity is also known).
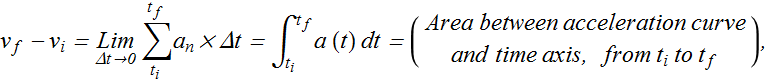
Here plot of time versus acceleration of a moving object (acceleration is not constant) is given.
Graphical methods are valid, whether acceleration is constant or not.